menu
search
知识点
登录
登录
七上总复习5
查看历史成绩
2026-01-11
填空题
1.
若分式 $\frac{2x-1}{x^2+2x+1}$ 的值为负数,则 x 的取值范围是 __________
错误
正确
填空题
2.
已知 $a^2+b^2-10a-6b+34=0$, 则 $\frac{3a^2-ab}{9a^2-6ab+b^2}$ = _____________
错误
正确
计算题
3.
提取公因式: $4(a-c)^2 - 2(c-a)^3$
错误
正确
填空题
4.
如图, $\triangle ABC$ 平移后能与 $\triangle DEF$ 重合,点 E 为 BC 上一点, BE=3cm,EC=8cm。 点 O 为 BC 上一点, BO=5cm,则点 O 可以沿 __________ 方向,平移 ________ cm到 O' 点, O'F 的长度为 ______ cm; 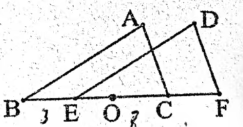
错误
正确
填空题
5.
将线段 AB 平移后得到线段 CD,点 A 与点 C 是对应点,若 AB 与 CD 在一条直线上,且 AB = 6, AD =2 ,则平移距离为 __________
错误
正确
计算题
6.
$(\frac{a^2+1}{a-1}-a+1)\div\frac{4a^2}{a^2-1}$
错误
正确
填空题
7.
如图所示的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1个单位长度, $\triangle ABC $ 的三个顶点均在格点上,点 O,M也在格点上。要求只用无刻度的直尺,在给定的网格中按要求画图。 1)画出 $\triangle ABC$ 先向右平移 5 个单位长度,再向下平移5个单位长度后得到的 $\triangle A_1B_1C_1$ 2)画出 $\triangle ABC$ 关于直线 OM 对称的 $\triangle A_2B_2C_2$ 3)画出 $\triangle ABC$ 绕点 O 按顺时针方向旋转 90° 后得到的 $\triangle A_3B_3C_3$ 4)$\triangle ABC$ 的面积是 _________ 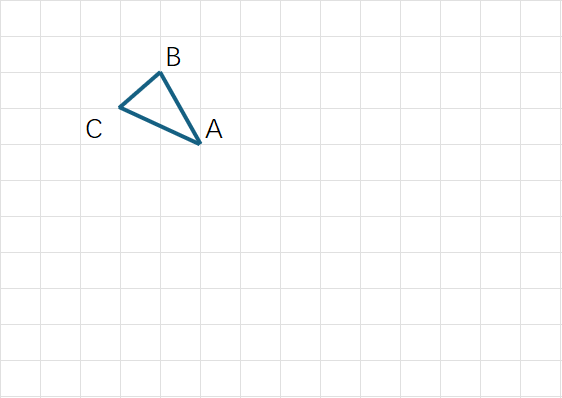
错误
正确
填空题
8.
定义:如果一个关于 x 的分式方程 $\frac{a}{x}=b$ 的解是 $x=\frac{1}{a+b}$ ,那么我们把这样的分式方程称为和解方程。例如方程 $\frac2x=-4$ 就是和解方程。已知关于 x 的分式方程 $\frac{n}x=2025-n$ 是和解方程,那么 n 的值是 ___________
错误
正确
填空题
9.
“数缺形时少直观,形缺数时难入微.数形结合百般好,隔裂分家万事休.”数形结合是解决数学问题的重要思想方法.通过计算几何图形的面积可以验证一些代数恒等式. 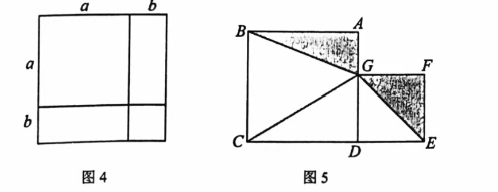 (1)如图4是一个大正方形被分割成了边长分别为a和b的两个正方形,长宽分别为a和b的两个长方形,利用这个图形可以验证乘法公式__________________. 利用上述公式解决问题: 【直接应用】 (2)若xy=3,x+y=5,则 $x^2+y^2$ = ___________ 【类比应用】 (3)若(x-20)(x-10)=15,求 $(x-20)^2+(x-10)^2$ 的值; 【知识迁移】 (4)如图5,在线段CE上取一点D(CD>DE),分别以CD、DE为边在线段CE同侧作正方形ABCD、DEFG,连接BG、CG、EG. 若阴影部分的面积和为 $\frac{85}2$ , $\triangle CDG$ 的面积为 $\frac{37}{2}$ ,则CE的长度是 ____________
错误
正确
填空题
10.
如图,在 $\triangle ABC$ 中,∠ACB=90°, AC=BC=1, 将 $\triangle ABC$ 绕A点逆时针旋转 30后得到 $\triangle ADE$ , 点B经过的路径为BD, 则图中阴影部分的面积是.(结果保留π) 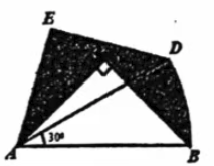
错误
正确
填空题
11.
已知 $(x+a)(x+b)=x^2+mx-9$, a,b为整数,能使这个等式成立的所有m的值是 ____________
错误
正确
填空题
12.
我们已经学习了整式乘法,可以计算以下的式子(如图5): 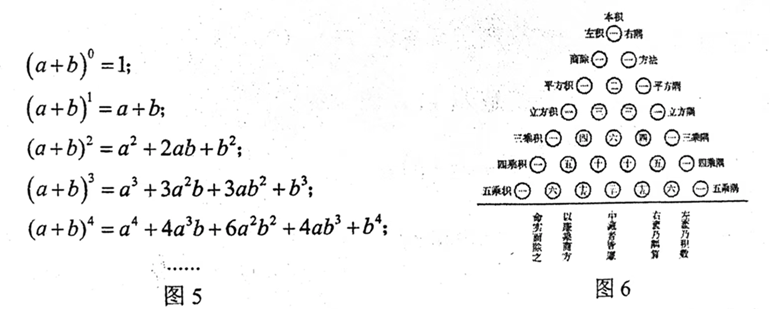 图5中各等式右边的各项系数的规律早在11 世纪就已被我国北宋数学家贾宪发现. 1261年,我国南宋数学家杨辉在他所著的《详解九章算法》中给出了一个“开方作法本源图”,如图6所示,并指明:“开方作法本源图出自《释锁算书》,贾宪用此术,”这幅图被后人称为“贾宪三角”. 请仔细观察“贾宪三角”,并根据其中蕴含的 $(a+b)^n$ 的系数规律,计算 $(x-2)^5$ 的展开式中 $x^3$ 项的系数是 __________
错误
正确
填空题
13.
解方程: $\frac{4}{x^2-6x+8}-\frac{1}{4-x}=\frac{4}{x-2}$
错误
正确
填空题
14.
.如图,分别以a,b,m,n为边长作正方形,且两个正方形有一条边在同一条直线上.已知m>n且满足am-bn=2,an+bm=4. (1) 如果a+b=3,ab=1,图7(左图)阴影部分的面积是 __________ (2) 图8(右图)中阴影部分的面积是 ____________________________ (用含 m、n的代数式表示); (3) 如果图7阴影部分的面积为4,图8中梯形 ABCD的面积为 5,求图8中阴影部分的面积. 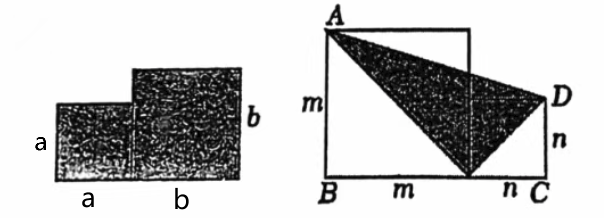
错误
正确
填空题
15.
如图,直角三角形 DEF 是直角三角形 ABC 沿射线 BC 方向平移所得到的,如果 AB=8, BE = 4, DH =3 ,那么图中阴影部分面积为 ________ 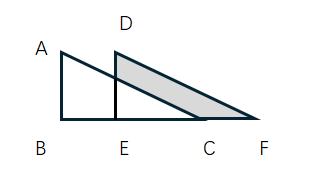
错误
正确
填空题
16.
用4张长为 a,宽为 b (b>a) 的长方形纸片,按如图的方式拼成一个边长为 (a+b) 的正方形,图中空白部分的面积为 $S_1$ ,阴影部分的面积为 $S_2$ 。若 $S_1=3S_2$ ,则 a 和 b 之间的数量关系是 _________ 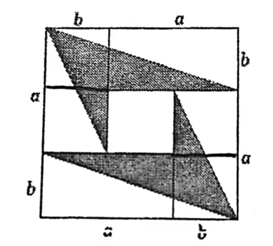
错误
正确
填空题
17.
$(-a^3)^{-2} \cdot (-a^2)^3$ = _________
错误
正确
填空题
18.
因式分解 $9(x+y)^2-(x-y)^2$
错误
正确
简答题
19.
已知 $3a-2b=0且 a\ne0$ ,先化简,再求 $(1+\frac{b}a-\frac{a}{a-b})\div(1-\frac{b}a-\frac{a}{a+b})$ 的值
错误
正确
填空题
20.
定义:如果两个代数式的和与这两个代数式的积相等,那么称这两个代数式互为“关联式” 1) 判断 $\frac2{x+1} 与 \frac2{x-1}$ 是否为互为“关联式”,并说出理由 2)求 $\frac1{2m+1}(m\ne0)$ 互为“关联式”的代数式. 3) $\frac{a}{bx+4}$ 与 $\frac{a}{x-1} (a\ne0)$ 互为“关联式”,求常数a和常数b的值
错误
正确
提交判题
沪ICP备2024105194号
沪公网安备31011702890224号
毛爸作品